|
MINIMISATION DE L'ÉCART QUADRATIQUE J
Rappels de cours
| Supposons que, suite à une
expérimentation, on dispose de n points Mi(ti,vi)
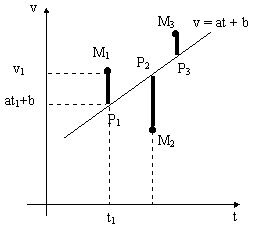
formant un nuage de points qui semble pouvoir être modélisé par une droite D
d'équation v = a* t + b Lorsque l'on substitue aux n points Mi(ti,vi) expérimentaux les points Pi (ti, a* ti + b) de la droite D, l'erreur commise sur chaque point est égale à MiPi = ½ vi -(a* ti + b)½ .On définit pour les n points expérimentaux Mi (ti,vi) l'écart quadratique moyen J par :
|
|
J mesure la moyenne des carrés de toutes les erreurs commises. La meilleure droite d'ajustement est celle correspondant à la valeur de J la plus petite possible.
Étude de J
1- quand expérimentalement b = 0
J est une fonction de a (notation mathématique J(a)). Étudions cette fonction :
![]()
J(a) = a a² - b
a + g avec ![]()
J est une fonction du second degré en a avec a
> 0.
J admet pour dérivée :
![]()
qui s'annule en changeant de signe pour ![]()
Donc pour cette valeur a0 la fonction J admet un minimum.
La meilleure droite de modélisation est donc la droite d'équation v = a0.t
Application numérique : étude cinématique de la chute libre
Dans le premier tableau ci-dessous, les 2 premières colonnes contiennent
les valeurs de ti et vi relevées lors du T.P. de sciences
physiques.
Le second tableau donne les valeurs de J(a) pour des valeurs de a variant entre 9.70 et
9.9 ce qui permet de repérer une valeur approximative de a pour laquelle J est minimum.
En appliquant les résultats mathématiques établis ci-dessus, calculer a0 :
![]()
![]()
La meilleure droite de modélisation a pour équation : ![]()
Retrouvez-vous la valeur a0 observée en T.P. de physique ?
2- lorsque b ¹ 0
J est alors une fonction de deux variables J(a, b). Les outils mathématiques pour étudier une telle fonction ne sont pas au programme de mathématiques de Terminale S mais ils existent cependant. On peut donc trouver a0 et b0 minimisant J.
Pour cela, il a été démontré que la meilleure droite d'ajustement D passe par le barycentre G(tG, vG) des n points Mi. On peut alors écrire : v = a(t - tG) + vG = a.t +(vG - a.tG)
La valeur a0 de a minimisant l'écart quadratique J peut être calculée comme précédemment. Il existe aussi des formules mathématiques donnant directement les valeurs a0 et b0. On peut les obtenir à l'aide de la calculatrice.
Extrait du premier tableau distribué aux élèves
t en s |
v en m.s-1 |
v/t |
t² |
t.v |
v² |
0,1394 |
1,39157 |
9,982568149 |
0,01943236 |
0,19398486 |
1,936467065 |
0,17189 |
1,68909 |
9,826575135 |
0,02954617 |
0,29033768 |
2,853025028 |
0,19902 |
1,95848 |
9,840619033 |
0,03960896 |
0,38977669 |
3,83564391 |
0,2224 |
2,18819 |
9,838983813 |
0,04946176 |
0,48665346 |
4,788175476 |
0,24384 |
2,40033 |
9,843873031 |
0,05945795 |
0,58529647 |
5,761584109 |
0,26427 |
2,5863 |
9,786581905 |
0,06983863 |
0,6834815 |
6,68894769 |
Extrait du deuxième tableau
a |
9,74 |
9,78 |
9,8 |
...... |
(v1-at1)² |
0,00114339 |
0,00079738 |
0,0006477 |
...... |
(v2-at2)² |
2,0867E-05 |
6,4093E-05 |
2,0867E-05 |
...... |
| (v3-at3)² | 6,5351E-05 |
0,00014555 |
6,5351E-05 |
...... |
| (v4-at4)² | 7,5169E-05 |
0,00017208 |
7,5169E-05 |
...... |
| (v5-at5)² | 0,00011445 |
0,00024257 |
0,00011445 |
...... |
(v6-at6)² |
1,2574E-05 |
3,0255E-06 |
1,2574E-05 |
...... |
...... |
...... | ...... | ...... | ...... |
J(a) |
0,00029088 |
0,00026737 |
0,00024131 |
...... |
![]()
Téléchargement de la fiche au format Word 97 Ecartq.doc (52 Ko)
INRP-TECNE
Unité Informatique et enseignement
06/06/2000