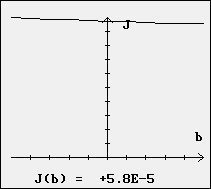|
|
MODÉLISATION
DU GRAPHE DE v(t)
OBTENU EN TP
Objectifs, place dans
la progression
Ce cours s'appuie sur les résultats obtenus par les élèves lors du TP précédent sur l'étude cinématique de la chute verticale d'une bille. Au cours de ce TP les élèves ont choisi "visuellement" la meilleure droite qui représente v(t) ; il s'agit ici de leur présenter une méthode mathématique pour déterminer cette droite : l'optimisation par la méthode des moindres carrés.
L'objectif visé à travers ce cours et le travail qui sera fait en mathématique est bien l'acquisition de connaissances théoriques sur une méthode d'optimisation d'un modèle et les conditions de son utilisation.
Les deux axes développés ici seront alors :
- Introduction de l'écart quadratique moyen et de sa minimisation
- L'utilisation de l'écart quadratique moyen pour trouver le "meilleur" modèle.
Remarque : Les éléments théoriques du cours présenté ci-dessous sont repris dans une fiche donnée aux élèves.
Introduction de l'écart quadratique moyen et de sa minimisation
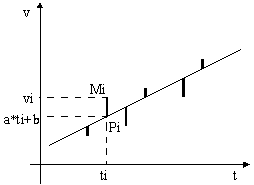
Dans l’étude cinématique de la chute libre, on dispose de n points expérimentaux Mi (ti,vi). L’allure du nuage de points semble que l’on puisse modéliser la relation entre v et t au moyen d’une droite affine t ® at + b.
On obtient alors en superposition les points expérimentaux Mi et le graphe de la fonction v = a* t+b Modéliser revient à substituer à chaque point expérimental Mi (ti,vi) un point théorique de même abscisse ti : Pi (ti, ati+b) L’erreur commise sur chaque vitesse est alors MiPi = | vi - a* ti + b| Le modèle sera le meilleur si la somme de toutes les erreurs commises est la plus petite possible. |
 |
Mathématiquement on peut calculer, pour n points expérimentaux, un écart quadratique moyen J, dépendant des valeurs choisies pour a et b et défini par :
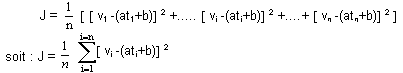
La droite de modélisation passe "au mieux" entre les points expérimentaux lorsque J est minimum.
En reprenant le logiciel CHUTE et le fichier de mesures réalisé en TP, on peut s’aider du calcul de J fait par le logiciel en fonction des valeurs proposées pour a et b. On obtient J minimum pour les valeurs de a et de b correspondant au meilleur modèle.
Il existe des conditions pour l'utilisation de la méthode "des moindres carrés" :
- pas d'incertitude sur la grandeur en abscisse (ou incertitude très faible),
- incertitude constante pour toutes les valeurs de la grandeur en ordonnée.
Ces conditions sont-elles réunies ici, a priori ?
Application
à l'optimisation du modèle v = a*
t+b
On réalise ensuite des essais successifs en prenant en compte les résultats obtenus par les élèves en TP et on relève les modifications entraînées sur J(a) et J(b).
Premier essai
| On choisit des valeurs issues du tableau de mesures pour
proposer a = 9,9 et b = 0. On observe la superposition des points expérimentaux et du modèle |
 |
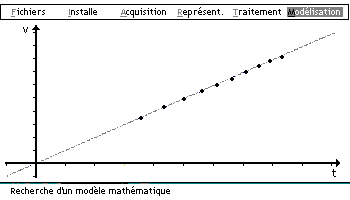Les valeurs de J(a) et le graphe correspondant permettent de repérer la valeur a0 qui minimise J(a).
 |
 |
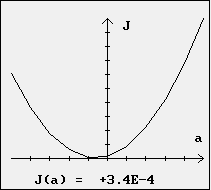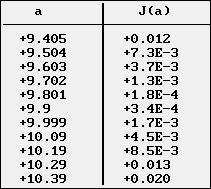Il en est de même pour la valeur b0 qui minimise J(b).
 |
 |
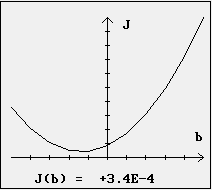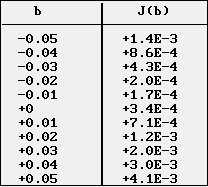On obtient sur cet exemple, a0 = 9,8 m.s-2 et b0 = - 0,01 m.s-1 .
Deuxième essai
Il peut être alors intéressant de montrer les modifications entraînées sur les écarts quadratiques (J(a) et J(b)) quand on change l'une des valeurs des paramètres du modèle.
On modifie ici la valeur de a et l'on prend a = 9,8 (avec b = 0).
On obtient les résultats suivants :
 |
 |
 |
 |
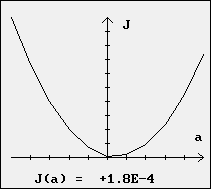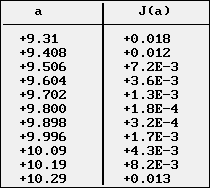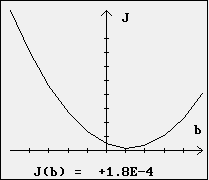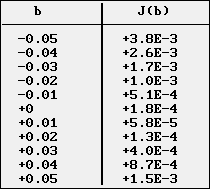On utilise cette fois la valeur b = + 0,01 qui minimise l'écart quadratique J(b) précédent et l'on obtient alors le tableau de valeurs et la représentation pour J(b) ci-dessous :
|
 |
La valeur de b est-elle
significative ?
Cette question est alors posée et discutée.
INRP-TECNE
Unité Informatique et enseignement
04/04/2000