|
|
MODÉLISATION DES OSCILLATEURS : QUELQUES EXEMPLES
La résolution numérique des équations différentielles, auxquelles amènent les modèles théoriques, permet de réaliser une exploitation qualitative avec les élèves de Terminale S.
Nous présentons succinctement ci-dessous un ensemble de situations bien connues concernant les oscillateurs, les résultats affichés ont été obtenus avec le logiciel de mathématiques Graph'X (SOFTIA).
Modélisation de
l'oscillateur linéaire
Équation différentielle : y’’(t) + Ay’(t) + w 02y(t) = 0 (A et w 0 constants)
Pour simplifier ici on pose w 0 = 1.
Cas de l’oscillateur libre non amorti : A = 0
Équation différentielle : y’’(t) = -y(t)
L’oscillateur est harmonique (oscillations sinusoïdales de période T0 = 2p /w 0).
La courbe de y(t) est représentée en pointillé dans le graphe ci-dessous (conditions
initiales : y0 = 0 y’0 = 2).
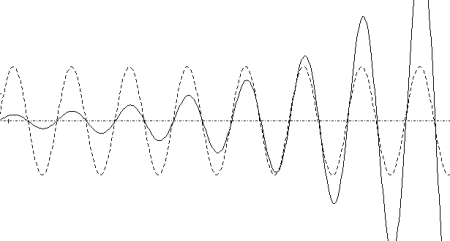
Cas de la naissance des oscillations : A < 0
Équation différentielle : y’’(t) = -Ay’(t) - y(t)
La courbe en trait plein ci-dessus est obtenue en choisissant A = - 0,15
(conditions initiales : y0 = 0 y’0 = 0,2).
On note que ce cas traduit un apport d'énergie.
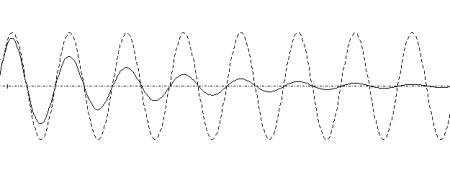
Cas de l’oscillateur libre amorti : A >0
Équation différentielle : y’’(t) = -Ay’(t) - y(t)
La courbe en trait plein ci-dessous est obtenue en choisissant A = + 0,15
(conditions initiales : y0 = 0 y’0 = 2).
On met alors en évidence l'existence d'une dissipation d'énergie.
Remarque : si A augmente, il peut y avoir disparition des oscillations ; le régime est alors apériodique.
Modélisation
de l'oscillateur de Van der Pol
Équation différentielle : y’’(t) - e [1 - y2(t)/a2 ]y’(t) + w 02y(t) = 0
C’est un oscillateur non linéaire : le facteur de y’(t) n’est pas constant (il dépend de y).
Pour simplifier, on pose a = 1 et w
0 = 1
L’équation s’écrit alors y’’(t) = e
[1 - y2(t)]y’(t) -y(t)
Avec les conditions initiales : y0 = 0 et y’0 = 0,01 on obtient les graphes ci-dessous :
Premier cas : e = 0,5
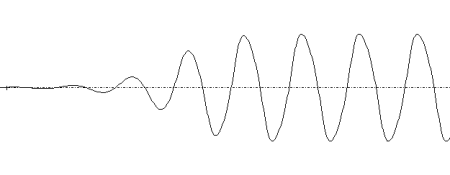
Les oscillations établies sont quasi sinusoïdales.
Deuxième cas : e = 5
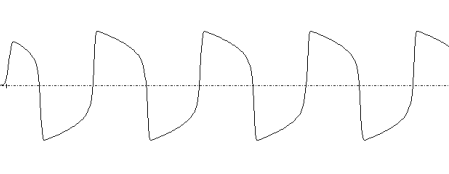
Les oscillations établies ne sont pas sinusoïdales.
Unité Informatique et enseignement
11/05/2000