DES MOINDRES CARRÉS ?
|
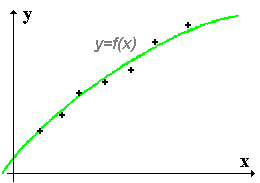
Un mesurage a conduit à N relevés de couples de mesures (x, y). Ils sont représentés par des points dans le graphe (x, y). Cet ensemble de points peut être représenté par une fonction mathématique
On cherche les valeurs des paramètres de la fonction de façon que la courbe passe au mieux dans l'ensemble des points expérimentaux. |
|
Le
choix d'un critère d'ajustement
On peut prendre comme mesure de l'écart entre la courbe mathématique et les points expérimentaux, la somme moyennée sur N mesures des écarts calculés pour chaque point et élevés au carré :
avec
Rechercher ce minimimum c'est chercher les "moindres carrés"...
Le cas particulier d'une fonction affine est appelé régression linéaire. Mais on peut également utiliser des régressions polynomiales.
Remarques :
- On ne peut faire une simple somme algébrique des écarts puisque celle-ci pourrait être nulle par le simple de jeu des compensations plus/moins.
- La solution la plus simple du point de vue mathématique consiste à prendre le carré.
- Par ailleurs, ceci rend compatible la mesure de l'écart quadratique avec la définition de l'écart-type.
- On divise par N ce qui permet de rapporter l'écart au nombre de mesures,.sinon l'écart augmente nécessairement avec le nombre de mesures.
- Si la fonction n'est pas linéaire par rapport aux paramètres, alors seules des méthodes itératives par approximations successives peuvent être utilisées.
- La fonction mathématique peut être quelconque.
- Ce qui est important c'est de comprendre que la nature de la fonction est définie a priori à partir d'une modélisation théorique.
- Le seul cas où l'on peut raisonnablement inférer une fonction mathématique au seul vu des points expérimentaux est celui où les points laissent penser à un alignement.
Le
principe des méthodes itératives
|
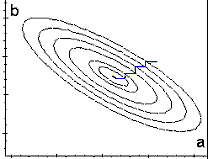
Ci-contre, sont représentées les courbes d'égale valeur de l'écart quadratique ({courbes iso-critère}) pour le cas de deux paramètres. L'algorithme consiste à examiner la variation de l'écart lorsqu'on modifie successivement a et b. Si l'écart diminue, on réitère les variations de a et de b. Si les valeurs initiales du calcul sont proches des valeurs cherchées, l'itération peut converger vers une valeur proche du minimum de l'écart quadratique. |
|
|
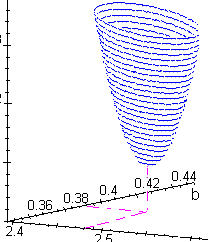
La courbe précédente peut être considérée comme la projection sur le plan (a, b) des coupes de la fonction J(a, b) par des plans horizontaux. Courbes analogues des courbes isobares |
|
Des
conditions d'utilisation ?
L'écart quadratique ainsi défini ne compte que les différences suivant l'axe des ordonnées. Cela sous-entend que l'incertitude sur la variable portée en abscisse est nulle ou négligeable.
De plus, il est constitué de la somme de tous les termes sans pondération. Cela sous-entend que l'incertitude (absolue) sur la grandeur portée en ordonnée est constante.
Ces deux points sont donc deux conditions d'utilisation de la méthode des moindres carrés simple (la régression linéaire en particulier) en tant qu'estimateur des paramètres du modèle. Il faut utiliser soit une méthode des moindres carrés pondérée, dite méthode du khi-deux (lorsque l'incertitude sur Y n'est pas constante) soit une méthode plus générale comme celle des ellipses (lorsque les deux variables ont des incertitudes).
Remarques :
Dans de nombreuses situations, on est amené à porter sur les axes, non pas la grandeur mesurée, mais une grandeur calculée à partir de celle-ci. C'est le cas lorsqu'on étudie l'énergie cinétique à partir de la mesure de la vitesse, ou lorsqu'on porte 1/p' pour l'étude des formules de conjugaison en optique.
Il faut bien voir que ceci sous-entend que l'on connaît déjà une grandeur ou une relation pour justifier le changement de variable. L'autre point important est que, si l'incertitude sur la mesure de la grandeur de base est constante, elle ne l'est plus sur son carré, son logarithme, etc. L'utilisation de la méthode des moindres carrés simple en tant qu'estimateur n'est donc pas possible.