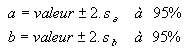QUEL EST LE LIEN AVEC LES INCERTITUDES EXPÉRIMENTALES ?

Les hypothèses sur les incertitudes permettent de minimiser l'écart quadratique compté suivant Oy. La valeur "résiduelle" est alors représentative des fluctuations aléatoires ; on obtient donc ainsi une estimation de l'incertitude sur chacune des mesures yi.Le minimum de l'écart quadratique est donc représentatif des erreurs aléatoires qui affectent les mesures.

L'utilisation de la méthode des moindres carrés entraîne donc une détermination de l'incertitude (supposée constante) sur la grandeur portée en ordonnée. Cette valeur est l'estimation de l'écart-type correspondant.
Pour un modèle à K paramètres

Toute détermination par une méthode statistique portant sur un échantillon n'est qu'une estimation. Cela sous-entend que le résultat ne peut être donné qu'avec une "fourchette", un intervalle, et que la valeur cherchée appartient à cet intervalle avec un certaine probabilité. En conséquence, les paramètres déduits de ces valeurs expérimentales affectées d'une incertitude sont donc eux-mêmes calculés avec une incertitude représentée par un écart-type que l'on peut estimer.

Pour la régression linéaire il est possible de calculer les valeurs de sa et sb. On devra donc écrire, pour N >15 mesures :
Un logiciel tel Excel (Microsoft), par exemple, fournit les résultats de la régression sous forme d'un tableau (commande dite matricielle) :

Comme dans le cas du traitement d'une seule grandeur, les valeurs obtenues sont des estimations à partir d'un nombre fini N de couples de mesures. L'intervalle de confiance est donc fonction du taux que l'on se fixe. Si le nombre de mesures est faible, il faut tenir compte d'un terme correcteur : le coefficient de Student t{N-2},%.

Ceci signifie qu'il faut prendre dans la table des coefficients de Student celui qui correspond au taux de confiance choisi et à l'indice N-2 qui représente le degré de liberté : nombre de mesures diminué de 2 du fait qu'il y a deux paramètres à déterminer (donc deux relations).