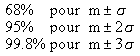ESTIMATEUR, TAUX DE CONFIANCE, ... C'EST-À-DIRE ?
 Généralités
Généralités
Un estimateur statistique est une grandeur mathématique calculée sur un ensemble de données et dont la valeur converge vers la valeur cherchée quand le nombre de données augmente.
Ceci sous-entend naturellement certaines propriétés des données...
Ainsi, la moyenne est un estimateur de la valeur cherchée si les mesures sont indépendantes et appartiennent à une même population statistique.
Toute détermination par une méthode statistique portant sur un échantillon n'est qu'une estimation. Cela sous-entend que le résultat ne peut être donné qu'avec une "fourchette", un intervalle, et que la valeur cherchée appartient à cet intervalle avec un certaine probabilité.
Le taux de confiance que l'on s'accorde est évidemment lié à la largeur de l'intervalle.
S'il existe des fluctuations ou erreurs aléatoires, une mesure ne peut fournir qu'une estimation de la valeur cherchée : la seule chose que l'on puisse dire est que la valeur cherchée se trouve probablement dans un intervalle autour de la valeur trouvée.
 Le
modèle de Gauss
Le
modèle de Gauss
La question est alors de savoir comment choisir l'intervalle et de savoir quelle confiance on peut s'accorder. Pour répondre à cela, il faut modéliser les incertitudes issues de fluctuations aléatoires.
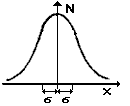
Le modèle utilisé en physique est la répartition gaussienne : on suppose que si l'on réitère N fois un même mesurage, pour lequel il existe une incertitude aléatoire (c'est-à-dire que les N résultats sont statistiquement indépendants), les mesures se répartissent, lorsque N croît, selon une courbe de Gauss.
|
Celle-ci est caractérisée par sa valeur centrale qui est la moyenne m et son étalement quantifié par une grandeur sigma nommée écart-type : |
|
|
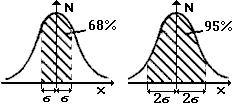
En termes de probabilité, cette répartition signifie que si l'on fait une mesure, il existe une probabilité précise qu'elle figure dans un intervalle donné. En particulier : |
|
On fait donc l'hypothèse que l'ensemble des mesures possibles peut être modélisé par une répartition gaussienne. De cet ensemble inconnu, la réalité expérimentale ne fournit donc qu'un échantillon à partir duquel il s'agit donc d'estimer la moyenne et l'écart-type.
Si les mesures sont bien des éléments de la même population, alors la moyenne de l'échantillon est le meilleur estimateur de la moyenne de la population et le meilleur estimateur de l'écart-type est :
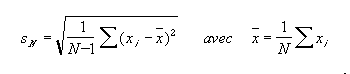
On notera que la relation n'est évidemment pas applicable lorsque N = 1...
Si le nombre de mesures est faible, l'estimation est évidemment moins bonne. En d'autres termes, puisqu'on n'utilise pas la moyenne et l'écart-type mais leurs estimations, l'intervalle de confiance doit en tenir compte : il est augmenté d'autant plus que le nombre de mesures est faible. On utilise pour cela un coefficient correctif : le coefficient de Student noté tn%. Ce symbole désigne le coefficient de Student à l'indice n, correspondant au taux de confiance % :
![]()