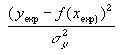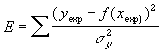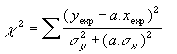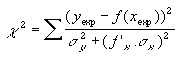QU'EST-CE QUE LA MÉTHODE DU KHI-DEUX ?
Une
nécessité bien naturelle
On peut se demander quelle est "l'importance" de l'écart calculé entre un point expérimental et le point théorique de même abscisse : comment dire s'il est grand, petit, raisonnable, aberrant ?
L'utilisation de l'écart relatif, c'est-à-dire rapporté à la valeur elle-même n'a pas de sens en général : une translation suivant Oy change évidemment cette valeur.
Et comment tenir compte de ce que, bien évidemment, il est plus important de faire passer une courbe près d'un point dont on est "sûr" que d'un point entaché d'une grande incertitude ?
Ce qui a du sens pour répondre à ces questions, c'est bien de comparer l'écart à l'incertitude connue ou estimée a priori...
|
Il faut donc calculer l'écart rapporté à cette incertitude, c'est-à-dire le rapport |
|
|
L'écart quadratique ainsi pondéré que l'on cherchera à minimiser est donc naturellement : |
|
Cette expression est désignée généralement par le calcul du khi-deux. Derrière ce nom à la consonance abstraite se cache donc une grandeur plus "naturelle" que l'écart-quadratique simple.
Comment
estimer les incertitudes ?
Suivant les protocoles utilisés :
- on pourra s'appuyer sur les indications du constructeur de l'appareil utilisé (les incertitudes indiquées par le constructeur correspondent à 3 écart-types de la population des appareils sortant d'usine).
- on devra effectuer une étude préalable du dispositif ou du protocole,
- on pourra appliquer une relation théorique connue : c'est le cas de l'étude des comptages en radioactivité. Si le comptage est suffisant, la loi de Poisson est proche d'une répartition gaussienne pour laquelle l'écart-type est proportionnel à racine du nombre de comptage.
Comment
faire s'il y a des incertitudes sur les deux grandeurs représentées ?
|
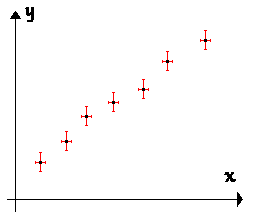
La première étape consiste à reporter les barres d'incertitude sur chaque point. En termes d'estimation statistique attachée à un taux de confiance,
il ne faut pas représenter les "rectangles En effet, la probabilité que le point cherché soit dans le coin, aussi bien qu'au voisinage d'une barre sous-entendrait que l'on a autant de chance d'avoir une valeur éloignée à la fois pour les deux mesures de x et y. À l'évidence ceci est moins probable... |
|
dits d'incertitude"
mais des ellipses 
. 
Pour calculer la meilleure estimation, il faut utiliser une méthode de type khi-deux généralisée qui tient compte de la relation entre y et x.
|
Dans le cas d'une fonction du type y = a.x + b, on comprend bien que l'incertitude à considérer sur y soit celle provenant de la mesure de y (sigma-y) et celle venant de la mesure de x (a.sigma-x). L'expression à minimiser est donc celle qui figure ci-contre. |
|
|
Dans le cas général, dans l'expression à minimiser (ci-contre) c'est localement la dérivée f ' de la fonction qui joue le rôle du paramètre "a" de l'expression précédente. |
|
