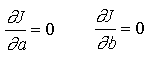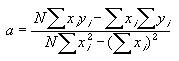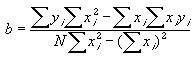D'OÙ VIENNENT LES FORMULES DE LA RÉGRESSION LINÉAIRE ?
POURQUOI Y-A-T-IL DES CONDITIONS D'UTILISATION ?
|
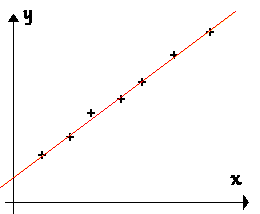
Un mesurage a conduit à N relevés de couples de mesures (xi, yi). Ces couples de mesures sont représentés par des points dans le graphe (x, y). Cet ensemble de points peut être représenté par une fonction affine y = a.x + b On cherche les valeurs des paramètres a et b de façon que la droite passe au mieux dans l'ensemble des points expérimentaux. |
|
La
minimisation d'un écart
Pour faire cet ajustement par calcul il faut se donner une mesure de l'écart entre la droite et les points expérimentaux. La meilleure droite sera celle qui minimise cette mesure.
Pour la régression linéaire, l'écart pour chaque point est la différence de coordonnées entre le point expérimental et le point théorique de même abscisse, et l'écart "total" est la somme de ces écarts élevés au carré, divisée par le nombre de mesures :
avec
Le minimum de J défini par l'annulation des dérivées partielles conduit aisément aux expressions analytiques de a et b.
|
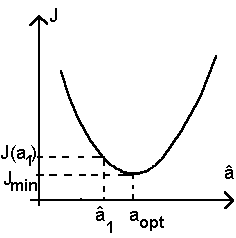
Il est facile de montrer l'existence d'un minimum de la fonction J(a,b) par rapport à l'un des paramètres. Le développement de J fait évidemment apparaître des termes en a et des termes en a au carré. L'expression générale de J(a) est donc celle d'une parabole :
qui présente évidemment un extrémum (un minimum car le coefficient m est positif). |
|
Pourquoi
y a-t-il des conditions d'utilisation ?
L'écart ainsi défini ne compte que les différences suivant l'axe des ordonnées. Cela sous-entend que l'incertitude sur la variable portée en abscisse est nulle ou négligeable.
L'écart fait la somme de tous les termes sans pondération. Cela sous-entend que l'incertitude (absolue) sur la grandeur portée en ordonnée est constante.
Ces deux points sont donc deux conditions d'utilisation de la régression linéaire en particulier en tant qu'estimateur des paramètres du modèle.
Remarques :
Dans de nombreuses situations, on est amené à porter sur les axes, non pas la grandeur mesurée, mais une grandeur calculée à partir de celle-ci. Il faut bien voir que ceci sous-entend que l'on connaît déjà une grandeur ou une relation pour justifier le changement de variable. L'autre point important est que, si l'incertitude sur la mesure de la grandeur de base est constante, elle ne l'est plus sur son carré, son logarithme, etc. L'utilisation de la régression linéaire en tant qu'estimateur n'est donc pas possible.
La régression linéaire est l'application de la méthode générale dite des moindres carrés.