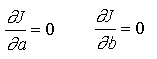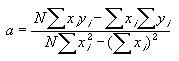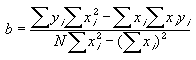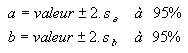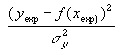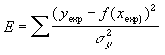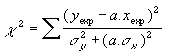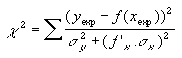À PROPOS DES MOINDRES CARRÉS
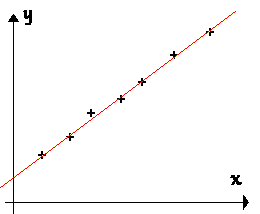
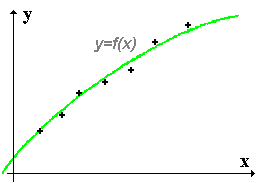
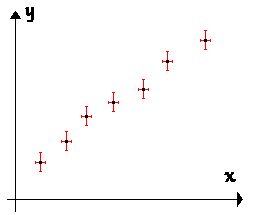
![]() Des points presque alignés... une régression linéaire ?
Des points presque alignés... une régression linéaire ?
| J'ai une série de mesures (x,
y). Je les ai représentées par un graphe (x, y). Les points montrent un certain
alignement. Je désire déterminer la valeur de la grandeur représentée par la pente de cette droite. Pour cela j'utilise la commande régression linéaire de ma calculette ou de mon logiciel.... |
|
![]() Une régression linéaire, pour quoi faire ?
Une régression linéaire, pour quoi faire ?
S'il s'agit d'obtenir une estimation visuelle de l'adéquation entre les mesures et un modèle linéaire, alors ce moyen est utilisable : ceci correspond à un "test" du modèle ; mais l'appréciation ne peut que rester qualitative.
S'il s'agit que d'une estimation rapide et approximative des valeurs des paramètres de la relation affine supposée, alors c'est souvent possible, mais il faut d'une autre manière déterminer les chiffres significatifs de chaque valeur.
S'il s'agit de déterminer des paramètres de la relation affine qui décrit les mesures, alors cela suppose que le modèle est fixé et que les incertitudes des mesures respectent certaines conditions. Sinon, il faut utiliser une autre méthode (de khi-deux, par exemple)
Si la relation peut être ramenée à une relation linéaire (y = a.x), et que l'objectif est de déterminer le paramètre a, alors il est préférable d'utiliser un autre protocole expérimental.
![]() Ai-je
le droit d'utiliser une régression linéaire ?
Ai-je
le droit d'utiliser une régression linéaire ?
En l'absence d'information sur les incertitudes des mesures, l'application de la régression linéaire n'est pas celle d'un estimateur statistique. Elle ne fournit donc a priori qu'une indication de l'ordre de grandeur des paramètres de la fonction modélisante. Il faut d'autres informations pour estimer les chiffres significatifs.
Si l'on peut faire l'hypothèse que les incertitudes sont négligeables sur la grandeur portée en abscisse et constante sur la grandeur portée en ordonnée, alors la régression fournit une estimation des paramètres a et b de la fonction affine représentative.
Ces estimations sont des valeurs accompagnées d'un intervalle de confiance. Par ailleurs, le calcul retourne une estimation de l'incertitude supposée constante sur les mesures portées en ordonnées.
![]() D'où viennent les formules de la régression linéaire ? Pourquoi y
a-t-il des conditions d'utilisation ?
D'où viennent les formules de la régression linéaire ? Pourquoi y
a-t-il des conditions d'utilisation ?
| Un mesurage a conduit à N
relevés de couples de mesures (xi, yi). Ces couples de mesures sont représentés par des points dans le graphe (x, y). Cet ensemble de points peut être représenté par une fonction affine y = a.x + b On cherche les valeurs des paramètres a et b de façon que la droite passe au mieux dans l'ensemble des points expérimentaux. |
|
Pour faire cet ajustement par calcul il faut se donner une mesure de l'écart entre la droite et les points expérimentaux. La meilleure droite sera celle qui minimise cette mesure.
Pour la régression linéaire, l'écart pour chaque point est la différence de coordonnées entre le point expérimental et le point théorique de même abscisse, et l'écart "total" est la somme de ces écarts élevés au carré, divisée par le nombre de mesures :
avec
Le minimum de J défini par l'annulation des dérivées partielles conduit aisément aux expressions analytiques de a et b.
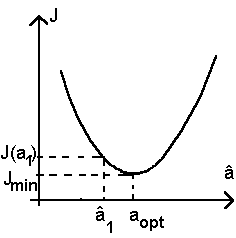
| Il est facile de montrer
l'existence d'un minimum de la fonction J(a,b) par rapport à l'un des paramètres. Le développement de J fait évidemment apparaître des termes en a et des termes en a au carré. L'expression générale de J(a) est donc celle d'une parabole :
qui présente évidemment un extrémum (un minimum car le coefficient m est positif). |
|
![]() Pourquoi y a-t-il des conditions d'utilisation ?
Pourquoi y a-t-il des conditions d'utilisation ?
L'écart ainsi défini ne compte que les différences suivant l'axe des ordonnées. Cela sous-entend que l'incertitude sur la variable portée en abscisse est nulle ou négligeable.
L'écart fait la somme de tous les termes sans pondération. Cela sous-entend que l'incertitude (absolue) sur la grandeur portée en ordonnée est constante.
Ces deux points sont donc deux conditions d'utilisation de la régression linéaire en particulier en tant qu'estimateur des paramètres du modèle.
Remarques :
Dans de nombreuses situations, on est amené à porter sur les axes, non pas la grandeur mesurée, mais une grandeur calculée à partir de celle-ci. Il faut bien voir que ceci sous-entend que l'on connaît déjà une grandeur ou une relation pour justifier le changement de variable. L'autre point important est que, si l'incertitude sur la mesure de la grandeur de base est constante, elle ne l'est plus sur son carré, son logarithme, etc. L'utilisation de la régression linéaire en tant qu'estimateur n'est donc pas possible.
La régression linéaire est l'application de la méthode générale dite des moindres carrés.
| Un mesurage a conduit à N
relevés de couples de mesures (x, y). Ils sont représentés par des points dans le
graphe (x, y). Cet ensemble de points peut être
représenté par une fonction mathématique On cherche les valeurs des paramètres de la fonction de façon que la courbe passe au mieux dans l'ensemble des points expérimentaux. |
|
![]() Le choix d'un critère d'ajustement
Le choix d'un critère d'ajustement
On peut prendre comme mesure de l'écart entre la courbe mathématique et les points expérimentaux, la somme moyennée sur N mesures des écarts calculés pour chaque point et élevés au carré :
avec
Rechercher ce minimimum c'est chercher les "moindres carrés"...
Le cas particulier d'une fonction affine est appelé régression linéaire. Mais on peut également utiliser des régressions polynomiales.
Remarques :
- On ne peut faire une simple somme algébrique des écarts puisque celle-ci pourrait être nulle par le simple de jeu des compensations plus/moins.
- La solution la plus simple du point de vue mathématique consiste à prendre le carré.
- Par ailleurs, ceci rend compatible la mesure de l'écart quadratique avec la définition de l'écart-type.
- On divise par N ce qui permet de rapporter l'écart au nombre de mesures,.sinon l'écart augmente nécessairement avec le nombre de mesures.
- Si la fonction n'est pas linéaire par rapport aux paramètres, alors seules des méthodes itératives par approximations successives peuvent être utilisées.
- La fonction mathématique peut être quelconque.
- Ce qui est important c'est de comprendre que la nature de la fonction est définie a priori à partir d'une modélisation théorique.
- Le seul cas où l'on peut raisonnablement inférer une fonction mathématique au seul vu des points expérimentaux est celui où les points laissent penser à un alignement.
![]() Le principe des méthodes itératives
Le principe des méthodes itératives
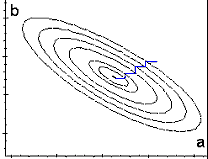
| Ci-contre, sont représentées les courbes
d'égale valeur de l'écart quadratique ({courbes iso-critère}) pour le cas de deux
paramètres. L'algorithme consiste à examiner la variation de l'écart lorsqu'on modifie successivement a et b. Si l'écart diminue, on réitère les variations de a et de b. Si les valeurs initiales du calcul sont proches des valeurs cherchées, l'itération peut converger vers une valeur proche du minimum de l'écart quadratique. |
|
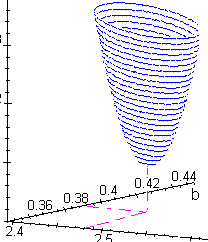
| La courbe précédente peut être considérée
comme la projection sur le plan (a, b) des coupes de la fonction J(a, b) par des plans
horizontaux. Courbes analogues des
courbes isobares |
|
![]() Des conditions d'utilisation ?
Des conditions d'utilisation ?
L'écart quadratique ainsi défini ne compte que les différences suivant l'axe des ordonnées. Cela sous-entend que l'incertitude sur la variable portée en abscisse est nulle ou négligeable.
De plus, il est constitué de la somme de tous les termes sans pondération. Cela sous-entend que l'incertitude (absolue) sur la grandeur portée en ordonnée est constante.
Ces deux points sont donc deux conditions d'utilisation de la méthode des moindres carrés simple (la régression linéaire en particulier) en tant qu'estimateur des paramètres du modèle. Il faut utiliser soit une méthode des moindres carrés pondérée, dite méthode du khi-deux (lorsque l'incertitude sur Y n'est pas constante) soit une méthode plus générale comme celle des ellipses (lorsque les deux variables ont des incertitudes).
Remarques :
Dans de nombreuses situations, on est amené à porter sur les axes, non pas la grandeur mesurée, mais une grandeur calculée à partir de celle-ci. C'est le cas lorsqu'on étudie l'énergie cinétique à partir de la mesure de la vitesse, ou lorsqu'on porte 1/p' pour l'étude des formules de conjugaison en optique.
Il faut bien voir que ceci sous-entend que l'on connaît déjà une grandeur ou une relation pour justifier le changement de variable. L'autre point important est que, si l'incertitude sur la mesure de la grandeur de base est constante, elle ne l'est plus sur son carré, son logarithme, etc. L'utilisation de la méthode des moindres carrés simple en tant qu'estimateur n'est donc pas possible.
![]() Quel est le lien avec les incertitudes expérimentales ?
Quel est le lien avec les incertitudes expérimentales ?
Les hypothèses sur les incertitudes permettent de minimiser l'écart quadratique compté suivant Oy. La valeur "résiduelle" est alors représentative des fluctuations aléatoires ; on obtient donc ainsi une estimation de l'incertitude sur chacune des mesures yi.Le minimum de l'écart quadratique est donc représentatif des erreurs aléatoires qui affectent les mesures.
| L'utilisation de la méthode des moindres carrés entraîne donc une détermination de l'incertitude (supposée constante) sur la grandeur portée en ordonnée. Cette valeur est l'estimation de l'écart-type correspondant. |
|
| Pour un modèle à K paramètres |
|
Toute détermination par une méthode statistique portant sur un échantillon n'est qu'une estimation. Cela sous-entend que le résultat ne peut être donné qu'avec une "fourchette", un intervalle, et que la valeur cherchée appartient à cet intervalle avec un certaine probabilité. En conséquence, les paramètres déduits de ces valeurs expérimentales affectées d'une incertitude sont donc eux-mêmes calculés avec une incertitude représentée par un écart-type que l'on peut estimer.
| Pour la régression linéaire il est possible de calculer les valeurs de sa et sb. On devra donc écrire, pour N >15 mesures : |
|
| Un logiciel tel Excel (Microsoft), par exemple, fournit les résultats de la régression sous forme d'un tableau (commande dite matricielle) : |
|
Comme dans le cas du traitement d'une seule grandeur, les valeurs obtenues sont des estimations à partir d'un nombre fini N de couples de mesures. L'intervalle de confiance est donc fonction du taux que l'on se fixe. Si le nombre de mesures est faible, il faut tenir compte d'un terme correcteur : le coefficient de Student t{N-2},%.
Ceci signifie qu'il faut prendre dans la table des coefficients de Student celui qui correspond au taux de confiance choisi et à l'indice N-2 qui représente le degré de liberté : nombre de mesures diminué de 2 du fait qu'il y a deux paramètres à déterminer (donc deux relations).
![]() Qu'est-ce que la méthode du khi-deux ?
Qu'est-ce que la méthode du khi-deux ?
On peut se demander quelle est "l'importance" de l'écart calculé entre un point expérimental et le point théorique de même abscisse : comment dire s'il est grand, petit, raisonnable, aberrant ?
L'utilisation de l'écart relatif, c'est-à-dire rapporté à la valeur elle-même n'a pas de sens en général : une translation suivant Oy change évidemment cette valeur.
Et comment tenir compte de ce que, bien évidemment, il est plus important de faire passer une courbe près d'un point dont on est "sûr" que d'un point entaché d'une grande incertitude ?
Ce qui a du sens pour répondre à ces questions, c'est bien de comparer l'écart à l'incertitude connue ou estimée a priori...
| Il faut donc calculer l'écart rapporté à cette incertitude, c'est-à-dire le rapport |
|
| L'écart quadratique ainsi pondéré que l'on cherchera à minimiser est donc naturellement : |
|
Cette expression est désignée généralement par le calcul du khi-deux. Derrière ce nom à la consonance abstraite se cache donc une grandeur plus "naturelle" que l'écart-quadratique simple.
![]() Comment
estimer les incertitudes ?
Comment
estimer les incertitudes ?
Suivant les protocoles utilisés :
- on pourra s'appuyer sur les indications du constructeur de l'appareil utilisé (les incertitudes indiquées par le constructeur correspondent à 3 écart-types de la population des appareils sortant d'usine).
- on devra effectuer une étude préalable du dispositif ou du protocole,
- on pourra appliquer une relation théorique connue : c'est le cas de l'étude des comptages en radioactivité. Si le comptage est suffisant, la loi de Poisson est proche d'une répartition gaussienne pour laquelle l'écart-type est proportionnel à racine du nombre de comptage.
![]() Comment
faire s'il y a des incertitudes sur les deux grandeurs représentées ?
Comment
faire s'il y a des incertitudes sur les deux grandeurs représentées ?
| La première étape consiste à
reporter les barres d'incertitude sur chaque point. En
termes d'estimation statistique attachée à un taux de confiance, il ne faut pas
représenter les "rectangles En effet, la probabilité que le point cherché soit dans le coin, aussi bien qu'au voisinage d'une barre sous-entendrait que l'on a autant de chance d'avoir une valeur éloignée à la fois pour les deux mesures de x et y. À l'évidence ceci est moins probable... |
|
Pour calculer la meilleure estimation, il faut utiliser une méthode de type khi-deux généralisée qui tient compte de la relation entre y et x.
| Dans le cas d'une fonction du type y = a.x + b, on comprend bien que l'incertitude à considérer sur y soit celle provenant de la mesure de y (sigma-y) et celle venant de la mesure de x (a.sigma-x). L'expression à minimiser est donc celle qui figure ci-contre. |
|
| Dans le cas général, dans l'expression à minimiser (ci-contre) c'est localement la dérivée f ' de la fonction qui joue le rôle du paramètre "a" de l'expression précédente. |
|
Unité Informatique et
enseignement
29/02/2000