QUELQUES OUTILS NUMÉRIQUES DE BASE
L’analyse de données expérimentales nécessite, dans de nombreux cas, la mise en œuvre de méthodes numériques informatisées : pour le chercheur, c'est en raison de la complexité intrinsèque des modèles étudiés, pour les élèves c'est aussi en raison de leur complexité relative, mais également en raison de la durée toujours limitée du temps de travail.
Trois grands types de méthodes sont présentés ici : le calcul et la représentation de grandeurs secondaires, le traceur de fonctions et la simulation numérique.
![]() Analyse et représentation des mesures
Analyse et représentation des mesures
Le calcul et la représentation de grandeur sont les techniques de base permettant d'effectuer des changements de variables (anamorphose) et de choisir l'espace de représentation adapté pour telle ou telle étude.
Ceci nécessite généralement, outre les quatre opérations élémentaires et les fonctions mathématiques, l'utilisation de méthodes de dérivation et d'intégration numérique appliquées à une série de points expérimentaux.
![]() Dérivation
numérique sur points expérimentaux
Dérivation
numérique sur points expérimentaux
Soit, par exemple, un ensemble de couples de mesures (xi, yi) entré à la main ou automatiquement dans l'ordinateur.
La méthode de base pour une dérivation numérique peut s'effectuer en utilisant la méthode connue des élèves depuis la classe de première :
y’i = (yi+1 - yi-1)/(xi+1 - xi-1)
Remarques :
- elle permet d'obtenir de bons résultats si les données initiales sont peu "bruitées" (faible dispersion), régulièrement espacées et suffisamment rapprochées ;
- les deux points extrêmes ne peuvent évidemment pas être calculés selon ce principe ; soit on donne simplement le résultat du calcul sur l'intervalle simple, soit on effectue une correction en tenant compte de la variation de la vitesse calculée sur les points voisins ;
- certains logiciels utilisent le calcul sur un intervalle simple pour l'ensemble des points ; des différences peuvent ainsi apparaître dans le calcul de dérivée par deux logiciels différents.
Une technique de "lissage" peut être utilisée pour estomper les effets "d’amplification de bruit" que l’on peut observer lorsque les points expérimentaux sont de qualité insuffisante :
| Lissage barycentrique, lorsque
les points sont régulièrement échantillonnés : on effectue un calcul pondéré
sur 5, 7, ... points, ce qui revient soit à faire une moyenne de dérivées soit à
remplacer les valeurs de yi+1 et yi-1 par une moyenne prenant en
compte les points voisins.
|
Vxi = (1/8dx)(yi+2 + 2yi+1- 2yi-1 - yi-2) |
| Lissage à partir d’une modélisation locale : on détermine un polynôme sur 5 points (par optimisation par exemple) puis on calcule la valeur de la dérivée analytique correspondante ; si les valeurs de a, b, c du polynôme y = ax2 + bx + c ont été déterminées de façon à passer au mieux par les cinq points xi+2, xi+1, xi, xi-1 , xi-2 (par minimisation d'un critère quadratique par exemple) alors la dérivée au point xi est obtenue en calculant : 2 axi + b | 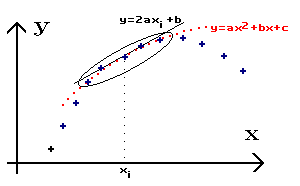 |
![]() Intégration
numérique sur points expérimentaux
Intégration
numérique sur points expérimentaux
La nécessité de calculer la (ou les) valeur(s) d'une primitive peut se rencontrer en mécanique pour le calcul du travail d’une force non constante ou celui d’une énergie (potentielle élastique), ainsi qu'en électricité pour le calcul de la charge à partir de l’intensité, par exemple.
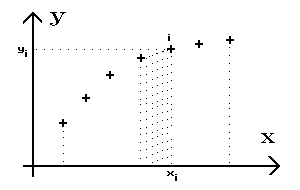
Le principe de la méthode élémentaire consiste à calculer l'aire comprise entre les points et l'axe des abscisses en considérant la somme S des aires des trapèzes consécutifs. Il s'agit alors d'une estimation des valeurs successives de l'intégrale définie dont la borne inférieure est le premier point et la borne supérieure la variable x courante :
| S(xi) = S si avec si = ½ (yi + yi-1)*(xi - xi-1) pour i de 2 à N et s1 = 0 |
 |
Remarque : on peut vouloir estimer l'intégrale à partir de x = 0 et non de la première mesure (cas du mouvement sur un plan incliné, par exemple). Dans ce cas il est possible d'utiliser une estimation de s1 par extrapolation : s1 = (a(½ x1) + b)*x1
![]() La confrontation des mesures à un modèle mathématique
La confrontation des mesures à un modèle mathématique
Pour analyser des données expérimentales, on est souvent amené à chercher la fonction mathématique qui représente (décrit) un ensemble de valeurs. La représentation pertinente ayant été choisie, il faut pouvoir tracer la courbe qui correspond à la fonction supposée.
| Le calcul est alors effectué sur
un nombre fini de valeurs de la variable "explicative" (même si la
représentation graphique donne un aspect continu !) et la courbe est tracée en
superposition des points expérimentaux. On ajuste à la main éventuellement l'un des paramètres (R expérimentalement mal déterminé, par exemple). |
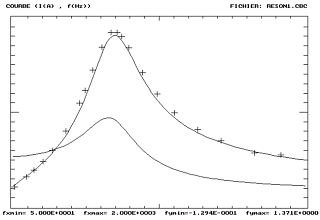 |
| Superposition des données expérimentales et du modèle théorique de I(f) complété par la courbe donnant Uc(f) |
Dans un certain nombre de cas, la confrontation graphique est insuffisante, et il convient de s'intéresser à un outil numérique permettant de quantifier l'adéquation du modèle par un critère numérique, l'écart quadratique par exemple.
| Un mesurage a conduit à N
relevés de couples de mesures (x, y). Ils sont représentés par des points dans le
graphe (x, y). Cet ensemble de points est censé
être représenté par une fonction mathématique On cherche s'il existe des valeurs des paramètres de la fonction tels que la courbe passe au mieux dans l'ensemble des points expérimentaux. |
|
On prend alors comme mesure de l'écart entre la courbe mathématique et les points expérimentaux, la somme moyennée sur N mesures des écarts calculés pour chaque point et élevés au carré :
![]() avec
avec ![]()
Rechercher ce minimimum c'est chercher les "moindres carrés"...
Cette méthode comporte des conditions d'utilisation si l'on souhaite faire une détermination fiable des paramètres. Il s'agit alors en effet d'une utilisation comme méthode d'analyse statistique des incertitudes.
![]() La résolution d'équations
différentielles
La résolution d'équations
différentielles
Dans un certain nombre de cas, l'application des relations fondamentales de la physique conduit à des équations différentielles qui, soit n'ont pas de solution analytique, soit sont rencontrées dans le cours de physique avant d'avoir été réellement traitées en mathématiques.
Une méthode numérique permet alors d'obtenir une solution point par point qui pourra être comparée aux données expérimentales.
Soit l'équation différentielle du premier ordre sur une fonction (inconnue) y(t) :
y' = dy/dt = f(t, y)
La résolution numérique consiste à calculer l'ensemble des valeurs prises par y à des dates successives :
to = 0, ..... , ti , ti+1 , .... (intervalle constant dt)
Si l'intervalle dt est suffisamment petit, on peut écrire :
yi+1 @ yi + y'i*dt avec y'i = f(ti, yi)
On voit ainsi que si yi est connu, alors yi+1 est calculable et qu'il suffit de donner une condition initiale : yo.
Pour une équation du second ordre, le même principe peut être utilisé. L'équation est du type :
y" = d²y/dt² = f(t, y, y' )
D'où l'on déduit :
yi+1 @ yi + y'i* dt
y'i+1 @ y'i + y"i* dt avec y"i = f(yi, y'i)
Il faut donc bien deux conditions initiales (yo et y'o) pour démarrer la résolution.
Cette méthode très simple peut être mise en œuvre sur un tableur. Elle est très instructive, mais n'est évidemment pas performante : les approximations successives entraînent rapidement une divergence des valeurs calculées.
Plusieurs méthodes peuvent être utilisées pour améliorer le calcul : la méthode de Feynman et celle, régulièrement utilisée, dite de Runge-Kutta.
![]() Méthode
de Feynman (équation du second ordre)
Méthode
de Feynman (équation du second ordre)
Elle consiste à utiliser l'estimation de la dérivée en i sur un intervalle double (i+1, i-1). Cela conduit à un calcul au second ordre :
y"i = f(yi, y'i )
y'i+1 = yi-1 + 2*y"i*dt
yi+1= yi-1 + 2y'i*dt
L'inconvénient, on le voit sur ces formules, est de nécessiter la connaissance, non seulement des conditions initiales classiques, mais également des valeurs correspondantes au point t1 : y1 et y'1. On doit alors utiliser un autre moyen pour les obtenir : autre mesure, calcul par développement de Taylor ou estimation au premier ordre.
![]() Méthode
de Runge-Kutta (cas d'une équation du premier ordre)
Méthode
de Runge-Kutta (cas d'une équation du premier ordre)
La même idée, mais poussée plus loin, permet encore d'améliorer le calcul. D'une part on obtient une expression polynomiale ne faisant intervenir que la fonction, et d'autre part, elle ne nécessite que la connaissance des conditions initiales à t = 0. Pour une équation du premier ordre la méthode est la suivante :
y' = dy/dt = f(t, y)
yi+1 = yi + 1/6(k0 + 2k1 + 2k2 + k3)
avec :
h = dt
k0 = h*f(ti, yi)
k1 = h*f(ti + h/2, yi + k0/2)
k2 = h*f(ti + h/2, yi + k1/2)
k3 = h*f(ti + h, yi + k2)
Une méthode équivalente existe pour les équations du second ordre, puisqu’on peut se ramener à deux équations différentielles du premier ordre en posant :
dy/dt = u
du/dt = f(t,y,u)
Les expressions correspondantes de la résolution numérique font donc intervenir deux jeux de paramètres :
ui+1 = ui + 1/6(k0 + 2k1 + 2k2 + k3)
yi+1 = yi + 1/6(l0 + 2l1 + 2l2 + l3)
On trouvera le détail du calcul de ki et li dans les nombreux ouvrages qui abordent ces techniques. Les exemples classiques sont l'oscillateur linéaire amorti, le pendule simple pesant et le circuit RLC. L'utilisation d'une méthode numérique permet alors d'obtenir le comportement théorique sans avoir à faire d'approximation rédhibitoire.
Unité Informatique et
enseignement
29/02/2000