Cette contribution s'inscrit dans le cadre de la recherche collective Approches co-disciplinaires des pratiques enseignantes dans leurs rapports aux apprentissages différentiels des élèves. Le corpus étudié est une séance ordinaire de mathématiques dans une classe de 5ème - au sens où elle n’a pas fait l’objet d’une ingénierie de recherche -, consacrée à la mise en place de la règle de la multiplication des fractions. Nous allons mettre en évidence des phénomènes didactiques dans cette classe de mathématiques dont nous pensons qu’ils dépassent le contexte de cette classe et de ce professeur.
  Nous commencerons par analyser la tonalité générale de cette leçon de 5ème sur les fractions en nous plaçant dans une perspective didactique. Nous identifierons notamment la nature de l’activité des élèves des élèves. Nous montrerons que la manière dont le professeur gère cette séance peut induire, à son insu, l’établissement dans la classe de rapports non adéquats à la vérité mathématique et au calcul numérique. Dans un deuxième temps, en étudiant plus précisément les interactions avec Mélanie, nous montrerons que cette élève est porteuse d’une résistance au contrat didactique.
  Pour analyser l’activité du professeur et des élèves dans cette séance, nous nous plaçons dans la perspective anthropologique du didactique développée Yves Chevallard (1998).
  Le contexte institutionnel de la séance observée
  Les programmes de mathématiques du collège ne présentent pas de cadre théorique dans lequel inscrire le travail sur les nombres rationnels et laisse un grand flou sur le statut des objets rencontrés. Les professeurs devant enseigner à leurs élèves les règles de calcul sur les fractions se trouvent devant une sorte de vide institutionnel comme nous l’avons aussi repéré à propos des nombres réels (Bronner 1997a et 1997b). Pour introduire ces objets d’apprentissage, un professeur doit choisir un cadre mathématique (Douady, 1986) dans lequel il propose une série de tâches à leur faire effectuer qui permettent, en faisant varier convenablement les variables à disposition, de parcourir la diversité des cas susceptibles d'être rencontrés et de faire émerger les objets visés. La leçon observée se place dans le cadre numérique et le calcul du produit de deux ou plusieurs fractions est présenté directement. Pour entrer rapidement dans l’organisation didactique de la leçon, nous proposons en annexe une trame de la séance en pointant un découpage temporel relativement aux différentes tâches proposées aux élèves.
  L’organisation didactique de la leçon
  Le professeur met en place une organisation didactique dans laquelle on peut dégager quatre moments (Chevallard, 1998) :
- un moment de première rencontre (minute 0 à 3) avec l’enjeu de la séance à partir du calcul de trois produits de fractions (5/6 x 7/6, 3/10 x 7/10, 2/11 x 3/7),
- un moment plus long (minute 3 à 21) d’élaboration d’une technique de calcul de ces produits et de quelques éléments permettant de justifier cette technique,
- un moment d’institutionnalisation de la technique (minute 21 à 27)
- et un moment d’exploration du type de tâche où le calcul portera sur le cas de plus de deux fractions et sur celui de fractions réductibles (minute 56).
  La première rencontre avec le type de tâche : le repérage d’une clause du contrat didactique à propos du calcul dans la classe de mathématiques
  Par la confrontation avec trois spécimens de produits de fractions, le professeur fait tout d’abord rencontrer aux élèves un type de tâches T1 : “ calculer le produit de deux fractions ” qui, en fait, n’est pas clairement identifiée, mais les élèves vont s’atteler sans ambiguïté à la “ tâche ” : “ mettre sous forme fractionnaire le produit de deux fractions ”, en raison d’un contrat complètement implicite que l’on pourrait expliciter de la façon suivante : “ Un calcul sur les fractions appelle un résultat fractionnaire et exact, sauf si d’autres précisions sont données ”. Le déroulement effectif de ce moment confirme cette analyse. Par exemple pour le calcul 5/6 x 7/6, l'enseignant interroge deux élèves et obtient les deux résultats sous forme fractionnaire : 35/6 et 35/36. Le calcul 3/10 x 7/10 aboutit également à la réponse erronée 21/10 et à la réponse correcte 21/100, tandis qu’une seule réponse (6/77) est produite par les élèves dans l’espace publique de la classe et relevée par le professeur.
  L'élaboration de la technique et des éléments technologiques : la non-dévolution de l’enjeu de la séance et le guidage du professeur
  Le traitement de ce moment nous permet à la fois de mieux saisir le choix des produits de fractions pour le professeur, mais aussi de préciser la tonalité didactique de l’enseignement observé. Pour permettre l'émergence de la règle le professeur provoque, à la suite de sa seule initiative, un changement de registre sur le second calcul (3/10 x 7/10) mettant en jeu des fractions décimales. Les élèves sont ainsi invités à passer dans le registre décimal et effectuent alors le calcul avec les techniques anciennes et stabilisées sur les nombres décimaux : 0,3 x 0,7 = 0,21. En fait, bien que l’égalité soit vraie, le résultat, écrit sous forme décimale, n’est pas la réponse attendue par l’enseignant compte tenu de son projet dans lequel la règle de multiplication des fractions semble être l’enjeu principal. Mais le professeur n’a pas fait la dévolution de la recherche des techniques aux élèves, il leur a seulement dévolué une tâche de calcul de fractions comme on l’a vu dans le premier moment. Aussi doit-il donner tout le cheminement à suivre aux élèves en leur précisant d'exprimer le résultat sous forme fractionnaire pour satisfaire son projet : 3/10 x 7/10 = 21/100. Après avoir demandé d’observer l’égalité obtenue, le professeur invite les élèves à “ expliquer ce qu’il fallait faire pour… effectuer le produit ” et à formuler une technique dans le registre verbal “ il fallait multiplier les numérateurs entre eux et les dénominateurs entre eux ”. Un élève, envoyé au tableau, viendra conclure cette phase en écrivant : .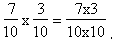
  Le milieu (Brousseau 1986), introduit par le professeur dans le premier moment, était insuffisant pour valider ou invalider une ou plusieurs réponses. C’est sans doute pour cette raison que celui-ci modifie alors le milieu en situation d’interaction avec le groupe classe en introduisant des écritures décimales. Mais cette initiative n’est du ressort que du seul professeur et le temps didactique ne pourra avancer qu’avec un guidage complet des actions mathématiques des élèves. L’élaboration de la technique qui commence à émerger va se poursuivre avec l’introduction par le professeur d’un nouvel élément : la calculatrice. La classe dispose de calculatrices permettant de donner les résultats sous forme fractionnaire. Le retour au premier exemple 7/6 x 5/6, traité à la calculatrice, va apparaître comme un nouvel élément de justification. Le professeur conduit les élèves à constater que la règle entrevue sur les fractions décimales reste valide pour des fractions quelconques. L’utilisation de la calculatrice s’arrête là, elle supplée l’autorité du professeur : le résultat que fournit la machine est indiscutable.
  Ainsi ce moment est un des plus significatif de la tonalité didactique qui se dégage dans cette séance.
  L’activité des élèves
  Au-delà du cas de cette leçon étudiée, on peut voir à l’œuvre ici une certaine lecture par le professeur du rapport institutionnel à l'activité mathématique. Le professeur semble souhaiter que le comportement de ses élèves - et donc sa gestion - soit conforme à une pédagogie active préconisée par les instructions officielles. Il propose une organisation pédagogique qui peut être qualifiée de “ classe dialoguée ”. Les exercices à résoudre individuellement sont ponctués de corrections collectives au tableau, le professeur s'appuie sur quelques réponses d'élèves à ses propres questions pour présenter une institutionnalisation de la règle de multiplication des fractions. Le professeur semble encore s’inscrire dans la pédagogie active préconisée par l’institution en proposant une forme d’expérimentation qui s’appuie sur les résultats de la calculatrice. Mais si l'on peut voir les élèves faire, ou essayer de faire, des calculs, et donc, comme on dit “ participer ”, ou en encore “ être en activité ”, on peut se demander quelle activité mathématique ils pratiquent, et quelles mathématiques ils construisent. Des injonctions institutionnelles poussant à faire participer les élèves à la réalisation d’une activité de nature mathématique, il y a un fossé que les instructions ne semblent pas permettre de combler facilement. Le professeur propose des "mini tâches" calculatoires, les élèves sont de simples exécutants, qui effectuent des calculs numériques sans avoir vraiment la possibilité de se confronter par eux-mêmes au problème posé qui n'a d'ailleurs jamais été explicitement présenté. De plus, l'enseignant ne laisse pas aux élèves la possibilité de "s'emparer" de la question en ne leur dévoluant à aucun moment la recherche de la validité des réponses.
  Le rapport à la vérité mathématique
À travers cet enseignement peut aussi se dégager un certain rapport épistémologique aux mathématiques, et plus précisément à la vérité mathématique. En effet, si l’expérimentation sur quelques exemples paraît une entrée dans la recherche intéressante, voire inéluctable, la généralisation du résultat et l’obtention de la règle, dans la gestion didactique choisie, risquent d’être confondues avec ce qui fonde un résultat mathématique c'est-à-dire une démonstration s’appuyant sur des résultats dûment explicités, même s'il est vrai qu’une telle preuve peut être difficilement fournie compte tenu du mode d’introduction des fractions au collège et des significations construites de ces objets. Dès le premier spécimen de produit de fractions, la règle est mise à jour, avec quelques précautions oratoires de la part du professeur, "donc, sur cet exemple", précautions vraisemblablement adressées davantage à lui-même qu’aux élèves. Tout au long de la séance et tout en restant dans la même forme de dialogue avec la classe, le professeur fait verbaliser la règle, ou s’en occupe lui-même. Cet énoncé va alors se naturaliser et va être officialisé à travers un ballet continu du type questions/réponses sans qu’une annonce publique lui donne vraiment un statut différent des autres énoncés qui ont été véhiculés dans la classe. La rupture de statut de l’énoncé sera difficile à repérer. L’institution attire pourtant fortement l’attention des enseignants sur ce point à propos des phases d’expérimentation : “ On veillera toutefois à ce que les élèves ne les confondent avec des démonstrations : par exemple, pour tout résultat mathématique énoncé, on précisera explicitement qu'il est admis lorsqu'il n'a pas été démontré ”(Instructions de collège, 1996).
  Le rapport au calcul
  On a vu plus haut, lors du moment de première rencontre, un premier élément du contrat didactique sur le calcul fractionnaire. Une autre clause implicite concernant le calcul va apparaître dans ce même moment : un calcul attend une et une seule réponse. Or si le résultat en tant que nombre est unique, il s'exprime par une expression numérique. Ainsi il est dénié dans l'action un fait incontournable de la réalité numérique : plusieurs expressions peuvent dénoter un même nombre, on parle alors d'expressions égales. Plus spécifiquement pour les nombres rationnels en jeu dans cette séance, il est possible de les exprimer par une infinité de fractions équivalentes. Cette éventualité n'est pas évoquée ici par l'enseignant.
  De plus, le professeur risque de laisser penser par sa formulation, bien sûr à son insu, que lorsqu'un calcul conduit à deux résultats différents, si l'un est faux, l'autre est nécessairement juste. Les élèves, quant à eux, semblent convaincus que s'il leur pose la question, c'est que le professeur sait que la bonne réponse est là. Ils doivent penser que si tel n'était pas le cas, il aurait questionné encore les élèves jusqu'à obtention de la bonne réponse parmi les réponses erronées. Au fil des échanges va ainsi ressortir une autre clause du contrat : d’une part, l’enseignant sollicite les élèves jusqu'au moment où il considère avoir assez de réponses dont la réponse attendue, en contrepartie, dans cette relation didactique, les élèves peuvent alors considérer que s’il s'est arrêté de questionner, la réponse fait partie du lot.
  Des ruptures de contrat
  Après l’institutionnalisation de la règle de multiplication de deux fractions, le professeur, dans la quatrième période, souhaite étendre la règle au produit de plusieurs fractions et pousser les élèves à obtenir les résultats sous forme de fractions irréductibles. Cette extension de la règle à un nombre plus important d’objets que celui présent dans l’institutionnalisation va apparaître sans qu’une annonce publique puisse être repérée. L’extension n’est jamais pointée, ni même évoquée, et elle semble aller de soi pour le professeur et peut-être pour une partie des élèves de la classe. Ce prolongement algébrique ne pose peut-être pas de difficulté à une partie des élèves, mais on verra qu’une élève Mélanie, dans le cas de quatre fractions, souhaite faire le calcul en les regroupant deux par deux. Les élèves devront donc décoder, à travers le contrat didactique qui émerge de façon singulière dans la classe, que cette règle s’étend naturellement : ce qui est vrai pour deux, l’est pour trois, quatre et plusieurs fractions.
  De manière analogue, les élèves devront aussi décoder les attentes du professeur à propos de la simplification au fur et à mesure du déroulement des derniers exercices alors que jusqu’ici, l’enseignant n’a jamais évoqué au cours de la séance la notion de fraction irréductible. Le professeur ne pourra atteindre complètement son but qu’en conduisant les élèves à simplifier et en les guidant pas à pas.
  Un exemple de relation didactique : le cas de Mélanie
  En dehors de la phase d’expérimentation initiale qui ne dure que trois minutes, le professeur ne prend pas en compte les résultats qu’ils soient erronés ou non. Lorsque l'élève interrogé pour la correction d'un exercice propose une procédure différente de celle attendue par le professeur, celui-ci ne laisse pas l'élève la développer, il interroge immédiatement la classe pour obtenir, semble-t-il, la méthode qu'il veut voir utilisée. On pourrait dire que le professeur est, en quelque sorte “ sourd ” à certains élèves, ou du moins qu’il est atteint d’une surdité sélective, n’entendant que les réponses conformes à son attente. Il est possible d'interpréter cette attitude comme une peur du professeur à engager la classe vers des erreurs qu’il ne saurait pas nécessairement bien gérer ou comme une crainte de laisser publique pendant un temps relativement long des réponses erronées qui pourraient s’imprimer dans la mémoire de certains élèves.
  Un passage significatif de ce phénomène est celui où Mélanie est envoyée au tableau pour la correction du calcul de E = 2/9 x 3/8 x 4/7 x 5/6 (minute 39 à 49). Lorsqu’elle manifeste son incompréhension, “ je ne comprends pas Monsieur ”, à propos de ce qu’elle doit faire au tableau, le professeur ne cherche pas à savoir ce qui lui pose problème. Cet aveu d’incompréhension audacieux de la part d'une élève provoque un discours fleuve du professeur dans lequel celui-ci fait à la fois les questions et les réponses. Ce discours a pour objet de décrire et d’expliciter “ sa ” propre démarche, démarche qu’il veut que les élèves suivent pour effectuer ce type de calcul. Pendant deux minutes, on assiste ainsi à une sorte de “ One Man Show ” du professeur, où fusent toutes les questions qu’il aimerait que les élèves se posent à propos de ce calcul, et qui aboutit pratiquement à un algorithme à mettre en œuvre “sans discussion” :
“ c'est pas clair ton explication on multiplie les numérateurs entre eux / puis on multiplie les dénominateurs entre eux alors vas-y applique cette règle ça fait / Minute 44 (Mélanie écrit: E = 2 x 3 x 4 x 5/9 x 8 x 7 x 6) voilà [5 secondes] bon / alors / qu'est-ce que tu vas faire maintenant / Mélanie ? est-ce que tu effectues tout de suite le produit au numérateur puis ensuite le produit au dénominateur / ou est-ce que tu fais / autre chose avant [5 secondes] au numérateur t'as un produit de facteurs d'accord tu as que des multiplications / hein ? au dénominateur / également / alors première question que je me pose / est-ce que je n'ai pas un facteur commun qui soit dans l'écriture du numérateur et en même temps dans l'écriture du dénominateur ? qu'est-ce que tu en penses ? (Mélanie fait non de la tête) non / est-ce qu'on ne pourrait pas en faire apparaître des fois / t'as pas des nombres là qui attirent Minute 45 / qui doivent / attirer ton attention ? ”
  Lorsque les élèves ne mettent pas en œuvre la procédure attendue, le professeur remet rapidement les élèves sur les rails de la résolution en leur imposant sa démarche. Cette décision peut avoir des origines très diverses comme l’évitement des incertitudes liées à la gestion de ce problème, le refus de voir des propos non valides exhibés dans la classe ou encore la volonté de reprendre les rênes en disant lui-même ce qu'il faut faire et comment il faut le faire. Cette manière de gérer les interactions va conduire Mélanie, malgré une certaine forme de résistance, à rester confinée dans une position de “ porte-voix ” du professeur. L'échange du professeur avec Mélanie commence comme une partie de ping-pong où apparaissent de nombreux effets Topaze (Brousseau, 1986). Voici un extrait de cet échange qui dure plus de dix minutes :
  Minute 46 quel est le nombre le facteur qui vient après ?
  Mélanie: 8
  L’enseignant : 8 est-ce que / est-ce que tu laisses 8 ou est-ce que tu mets autre chose à la place
  Mélanie: 4 fois 4 heu 4 fois 2
  L’enseignant : 4 que multiplie 2 / vas-y // ensuite est-ce que tu as d'autres transformations à faire ?
  Mélanie: il va y avoir 6
  L’enseignant : alors vas-y mais vas-y fais-le fais / écoute t'es toute empruntée là! allez dépêche-toi! // et le 7 qu'est-ce que t'en as fait ? tu l'as laissé tomber ? / le 7 ? // tu peux le mettre là mais je ne vois pas pourquoi bon enfin vas-y vas-y alors maintenant est-ce que tu as vu les simplifications qui avaient à faire
  Mélanie: oui
  L'enseignant :/ alors vas-y quelles / tu changes de craie pour les faire apparaître d'abord [5 secondes] oui // oui /// oui
  Minute 47 (Mélanie entoure les nombres) allez / là / est-ce qu'il y a d'autres simplifications ? (Au tableau on a: 2 x 3 x 4 x5/3x3x4x2x3x2x7)
  Mélanie: non
  Les questions sont fermées, rapprochées, souvent courtes et appellent des réponses se résumant souvent à un mot ou quelques mots. Le professeur ne laisse aucun espace à Mélanie pour la moindre réflexion. Mélanie est là pour écrire ce que le professeur attend, pour terminer les phrases de celui-ci sous le feu des questions. L'agacement que Mélanie semble provoquer chez le professeur va en s'accentuant, la tension semble monter. Le guidage de l’enseignant se traduit par un retour massif d’effets Topaze.

  Tous les éléments précédents - non-prise en compte des erreurs, des résultats, et des procédures, ou encore des incompréhensions déclarées - vont dans le sens d’une pédagogie donnant une impression globale de participation des élèves, mais où l’activité de ceux-ci se résument souvent à remplir les quelques “ blancs ”.
  Au-delà du cas singulier de cet enseignant, notre étude nous a permis de mettre en évidence des phénomènes qui sont, sans doute, assez répandus dans les classes de mathématiques au collège.

  BIBLIOGRAPHIE
  BRONNER A. (1997a), Étude didactique des nombres réels, idécimalité et racine carrée, Thèse, Université J. Fourier, Grenoble.
  BRONNER A., (1997b), Les rapports d’enseignants de Troisième et de Seconde aux objets “ nombre réel ” et “ racine carrée ”, Recherches en Didactique des Mathématiques, Volume n° 17.3, La pensée sauvage, Grenoble.
  BROUSSEAU G., (1986), Fondements et méthodes de la didactique des mathématiques, Recherches en Didactique des Mathématiques, Volume n° 7.2, La pensée Sauvage, Grenoble.
  DOUADY R., (1986), Jeux de cadres et dialectique outil-objet, Recherches en Didactique des Mathématiques, Volume n° 7.2, La pensée Sauvage, Grenoble.
  CHEVALLARD Y. (1998), Familière et problématique, la figure du professeur, Recherche en Didactique des Mathématiques (RDM), Vol 17/3, La pensée sauvage, Grenoble.