LA CONFRONTATION DES MESURES À UN MODÈLE MATHÉMATIQUE
Le
traceur de fonctions
Pour analyser des données expérimentales, on est souvent amené à chercher la fonction mathématique qui représente (décrit) un ensemble de valeurs. La représentation pertinente ayant été choisie, il faut pouvoir tracer la courbe qui correspond à la fonction supposée.
|
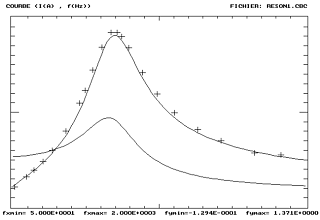
Le calcul est alors effectué sur un nombre fini de valeurs de la variable "explicative" (même si la représentation graphique donne un aspect continu !) et la courbe est tracée en superposition des points expérimentaux. On ajuste à la main éventuellement l'un des paramètres (R expérimentalement mal déterminé, par exemple). |
 |
|
Superposition des données expérimentales et
du modèle théorique
de I(f) complété par la courbe donnant Uc(f) |
L'écart
quadratique
Dans un certain nombre de cas, la confrontation graphique est insuffisante, et il convient de s'intéresser à un outil numérique permettant de quantifier l'adéquation du modèle par un critère numérique, l'écart quadratique par exemple.
|
Un mesurage a conduit à N relevés de couples de mesures (x, y). Ils sont représentés par des points dans le graphe (x, y). Cet ensemble de points est censé être
représenté par une fonction mathématique On cherche s'il existe des valeurs des paramètres de la fonction tels que la courbe passe au mieux dans l'ensemble des points expérimentaux. |
|
On prend alors comme mesure de l'écart entre la courbe mathématique et les points expérimentaux, la somme moyennée sur N mesures des écarts calculés pour chaque point et élevés au carré :
avec 
Rechercher ce minimimum c'est chercher les "moindres carrés"...
Cette méthode comporte des conditions d'utilisation si l'on souhaite faire une détermination fiable des paramètres. Il s'agit alors en effet d'une utilisation comme méthode d'analyse statistique des incertitudes.