ANALYSE ET REPRÉSENTATION DES MESURES

Le calcul et la représentation de grandeur sont les techniques de base permettant d'effectuer des changements de variables (anamorphose) et de choisir l'espace de représentation adapté pour telle ou telle étude.

Ceci nécessite généralement, outre les quatre opérations élémentaires et les fonctions mathématiques, l'utilisation de méthodes de dérivation et d'intégration numérique appliquées à une série de points expérimentaux.

• Dérivation numérique sur points expérimentaux
• Intégration numérique sur points expérimentaux

 Dérivation numérique sur points expérimentaux

Soit, par exemple, un ensemble de couples de mesures (x_i, y_i) entré à la main ou automatiquement dans l'ordinateur.

La méthode de base pour une dérivation numérique peut s'effectuer en utilisant la méthode connue des élèves depuis la classe de première :

y’_i = (y_i+1 - y_i-1)/(x_i+1 - x_i-1)

Remarques :

• elle permet d'obtenir de bons résultats si les données initiales sont peu "bruitées" (faible dispersion), régulièrement espacées et suffisamment rapprochées ;
• les deux points extrêmes ne peuvent évidemment pas être calculés selon ce principe ; soit on donne simplement le résultat du calcul sur l'intervalle simple, soit on effectue une correction en tenant compte de la variation de la vitesse calculée sur les points voisins ;
• certains logiciels utilisent le calcul sur un intervalle simple pour l'ensemble des points ; des différences peuvent ainsi apparaître dans le calcul de dérivée par deux logiciels différents.

Une technique de "lissage" peut être utilisée pour estomper les effets "d’amplification de bruit" que l’on peut observer lorsque les points expérimentaux sont de qualité insuffisante :

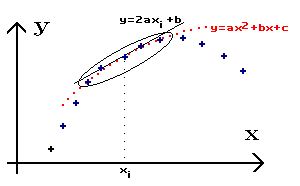
Lissage à partir d’une modélisation locale : on détermine un polynôme sur 5 points (par optimisation par exemple) puis on calcule la valeur de la dérivée analytique correspondante ; si les valeurs de a, b, c du polynôme y = ax2 + bx + c ont été déterminées de façon à passer au mieux par les cinq points xi+2, xi+1, xi, xi-1 , xi-2 (par minimisation d'un critère quadratique par exemple) alors la dérivée au point xi est obtenue en calculant : 2 axi + b

 Intégration numérique sur points expérimentaux

La nécessité de calculer la (ou les) valeur(s) d'une primitive peut se rencontrer en mécanique pour le calcul du travail d’une force non constante ou celui d’une énergie (potentielle élastique), ainsi qu'en électricité pour le calcul de la charge à partir de l’intensité, par exemple.

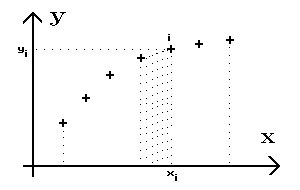
Le principe de la méthode élémentaire consiste à calculer l'aire comprise entre les points et l'axe des abscisses en considérant la somme S des aires des trapèzes consécutifs. Il s'agit alors d'une estimation des valeurs successives de l'intégrale définie dont la borne inférieure est le premier point et la borne supérieure la variable x courante :

S(xi) = S si avec si = ½ (yi + yi-1)*(xi - xi-1) pour i de 2 à N et s1 = 0

Remarque : on peut vouloir estimer l'intégrale à partir de x = 0 et non de la première mesure (cas du mouvement sur un plan incliné, par exemple). Dans ce cas il est possible d'utiliser une estimation de s₁ par extrapolation : s₁ = (a(½ x₁) + b)*x₁