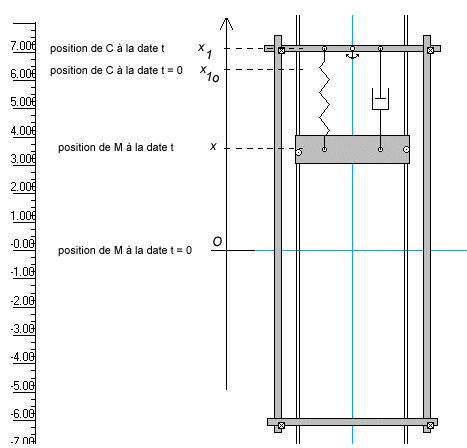
Notation des variables et valeurs numériques L'objet (M) de masse m = 4 kg, est situé à l'abscisse 0 à la date t = 0. Sa vitesse initiale est de + 23,826 m/s. Le caisson (C) a un mouvement imposé, ici sinusoïdal, d'équation x1 = x10 + A sin ( omega*t ) avec x10 = 6.56 m A = 0.57 m omega = 41.8 rad/s Le ressort de raideur k à une longueur à vide L0. k = 70 N/kg L0  = 6 m. sa longueur à la date t = 0 vaut 6.56 m L'amortisseur a une constante f. f = 1 N/(ms-1)

1. Etablissement de l'équation différentielle

   On se place dans un référentiel terrestre supposé galiléen . On précise que l'amortisseur exerce sur l'objet (M) une force dont la coordonnée sur l'axe vertical choisi est égale à - f ( dx/dt - dx1/dt ).
   Ecrire l'équation différentielle du mouvement et la mettre sous la forme : d²X/dt² + a dX/dt + b X = f ( t )
   

   Fiche réponse (après avoir téléchargé la fiche, vous pouvez l'imprimer si vous le désirez)

   
   Identifier X, a, b et la fonction f(t). Comparer notamment la période du mouvement du caisson et la période propre de l'oscillateur.

2. Vérifier vos calculs

   Cliquer ici avant de poursuivre

3. Application numérique

   Après la vérification, écrire l'équation différentielle obtenue en remplaçant a, b et f(t) par leurs valeurs numériques pour la résolution par Maple.

4. Résolution de l'équation différentielle avec MAPLE

Fiche Maple (après avoir téléchargé la fiche, vous pouvez l'imprimer si vous le désirez)

Cette fiche Maple est un fichier au format pdf et elle contient le travail à réaliser avec le logiciel Maple. (quelques indications pour résoudre une équation différentielle et obtenir le tracé de la solution).

Lancer le logiciel Maple (il est conseillé de fermer tous les autres logiciels ouverts) et effectuer le travail demandé. L'objectif est bien de retrouver les solutions proposées par le logiciel InteractivePhysique et ainsi de tester ces deux logiciels.

 

Éléments de solution