|
|||||||||
|
||||||||||
![]()
| La modélisation avec STELLA© |
Le logiciel Stella est fondé sur la construction de modèles reposant sur l'utilisation de 3 "objets" (réservoir, pompe, convertisseur, représentés par 3 symboles graphiques que sont le rectangle, la flèche et le rond) : affectation de grandeurs physiques aux objets ; création de liens directionnels traduisant les relations entre grandeurs mises en œuvre dans le modèle.
|
Cet ensemble pompe/réservoir est, du point de vue du calcul, un intégrateur par rapport au temps. |
Fonctionnant à un niveau abstrait, il permet de traiter de façon équivalente des systèmes mécaniques, électriques, etc., illustrant ainsi l'un des aspects de la modélisation : un même formalisme pour différents domaines.
On peut retrouver la loi de décomposition radioactive en modélisant l'hypothèse que le débit (négatif dans ce cas) dépend de la valeur du réservoir.
| Si on fait l'hypothèse d'une relation de simple
proportionnalité, on peut faire apparaître le paramètre de proportionnalité. Il suffit alors d'entrer dans "Taux" l'expression "lambda*N" qui explicite mathématiquement l'hypothèse. |
|
|
| Ainsi, sans résoudre l'équation différentielle, mais en traduisant
l'hypothèse que le taux de désintégration dépend, par une loi simple, de la quantité
de noyaux, on obtient l'évolution temporelle "classique". Dans l'exemple
ci-contre la valeur initiale de N a été prise égale à 1.50E12 et celle de lambda donne
une période de 30 années (Césium). Fichier : Cesium2.stm (7 ko) |
|
|
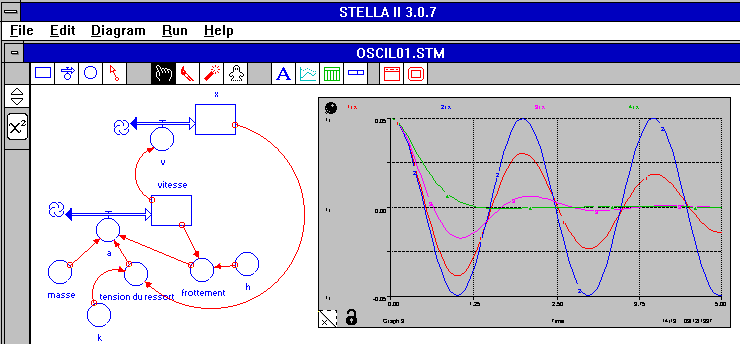
Stella est particulièrement adapté à la modélisation en mécanique. La vitesse étant la dérivée de la position par rapport au temps, celle-ci peut en effet être considérée comme le réservoir alimenté par la pompe vitesse. De même, l'accélération étant la dérivée de la vitesse par rapport au temps, celle-ci sera alors le réservoir alimenté par la pompe accélération. La résolution de l'équation différentielle du mouvement sera donc obtenue avec Stella en créant un tel double intégrateur numérique.
Pour un oscillateur mécanique à une dimension, par exemple, les forces appliquées peuvent être la tension du ressort T et une force de frottement f qui peut dépendre de la vitesse.
Un circuit électrique dans lequel sont branchés en série un générateur de tension, un conducteur ohmique, une bobine et un condensateur est décrit par une équation différentielle analogue à celle obtenue en mécanique. La même structure à deux intégrateurs sera donc utilisée pour obtenir la charge du condensateur : di/dt intensité, et intensité charge.
| La grandeur "dérivée de i" est bien évidemment reliée aux
différents paramètres E, L, R et C, mais aussi à la charge q et à l'intensité
i. Un tel modèle permet d'étudier aussi bien les oscillations libres amorties, auto-entretenues ou forcées : il suffit de spécifier le modèle choisi pour E. |
|
|
|
E = 0 ; oscillations libres (amorties suivant R) |
E est une fonction sinusoïdale ; oscillations forcées |
Fichier Stella : Rlcforce.stm (164 ko)
Des études, exemples, exercices, etc., peuvent être trouvées sous forme des "lettres" publiées sur le site Internet du CIP de Genève : http://wwwedu.ge.ch/cptic/clubs/modesimu/welcome.html/cip. Sinon, les publications sont essentiellement en langue anglaise.
4 mars 1998